第140回【Python】二次元区間和

現在取り組んでいるのは、paiza ラーニング問題集「クエリメニュー」になります。

はじめに

猫とキャンプと野球観戦と AWS が大好きな旦那、LeoSaki です。モフモフしたい。

Python をゼロから勉強してみよう、のコーナー 140 回目です。

Amazon Athena でごちゃごちゃ作業していることが多い今日この頃。結構なんだって出来ちゃうんだけれど、そのための方法がすぐに思いつかず、ネットの情報にしがみついています。LeoSaki（旦那）も困っているどなたかの参考になれればいいのですが。

それでは、今日も頑張ってみようと思います。

二次元区間和

H 行 W 列 の行列 A の 2 つの行・列番号の組 {a , b} , {c , d} における区間和 S({a,b} , {c,d}) (a ≦ c , b ≦ d) を以下の数式・図の通り定義します。以後 A の y 行 x 列の要素を A[y][x] と表すことにします。

S({a,b} , {c,d}) = A[a][b] + A[a][b+1] + … + A[a][d] + A[a+1][1] + … + A[a+1][d] + … + A[c][1] + … + A[c][d]

例として、入力例 1 の A における S({2,2},{3,3}) は以下の通りになり、値は 28 となります。

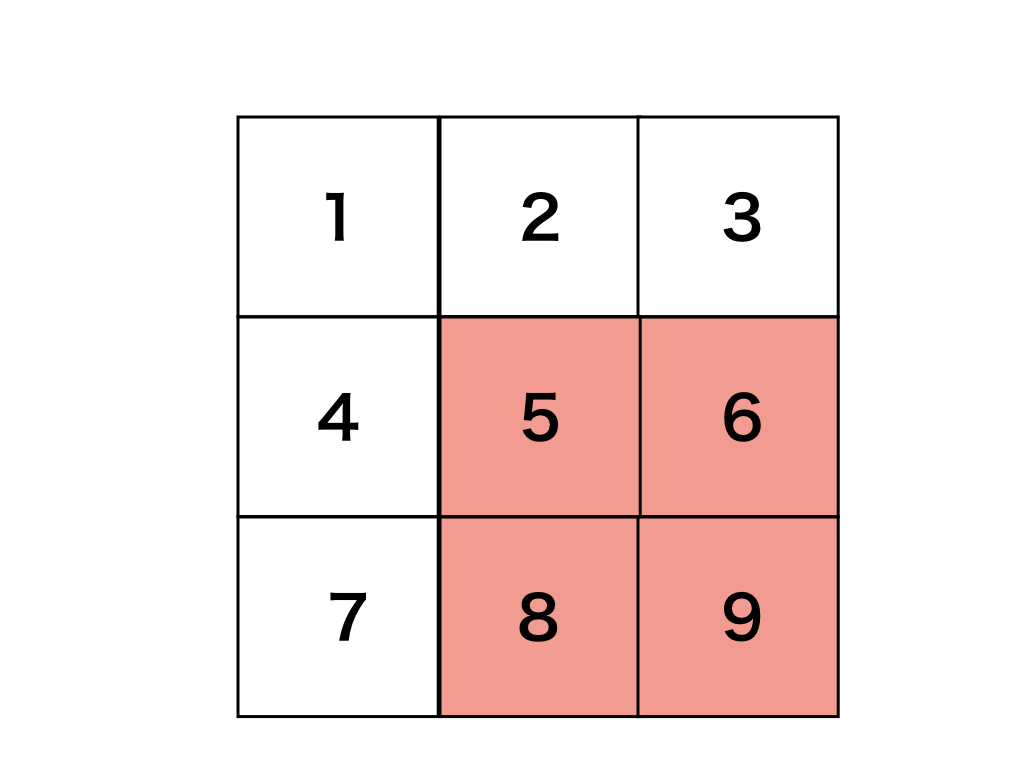
H 行 W 列 の行列 A と、区間和を求めたいペアについての情報が与えられるので、各ペアについて累積和を求めてください。

H W N
A[1][1] ... A[1][W]
...
A[H][1] ... A[H][W]
a_1 b_1 c_1 d_1
...
a_N b_N c_N d_N

・1 行目では、配列 A の行数 H と列数 W , 与えられる整数のペアの個数 N が与えられます。
・続く H 行のうち i 行目では、行列 A の i 行の要素が半角スペース区切りで A[i][1] から順に与えられます。
・続く N 行のうち i 行目では、累積和を求めるのに使う 2 つの行番号・列番号のペア {a_i , b_i} {c_i , d_i} が与えられます。

期待する出力

ans_1
...
ans_N

・i 行目に区間和 S({a_i,b_i} , {c_i,d_i}) の値 ans_i (1 ≦ i ≦ K)を出力してください。
・また、出力の末尾には改行を入れてください。

すべてのテストケースにおいて、以下の条件をみたします。

・1 ≦ H , W ≦ 1,000
・1 ≦ N ≦ 100,000
・-100 ≦ A[i][j] ≦ 100 (1 ≦ i ≦ H , 1 ≦ j ≦ W)
・1 ≦ a_i ≦ c_i ≦ H (1 ≦ i ≦ N)
・1 ≦ b_i ≦ d_i ≦ W (1 ≦ i ≦ N)

入力例

3 3 2
1 2 3
4 5 6
7 8 9
1 1 3 3
1 2 2 3

出力例

45
16

結構複雑に見えて、仕組みを理解すれば難しくない、と思う。最初の頃はいつも必死になって紙に図形を書いていた気がする。

Python
H,W,N = map(int,input().split())
A = [[int(x) for x in input().split()] for _ in range(H)]
ans = [[0] * (W+1) for _ in range(H+1)]

for i in range(1,H+1):
    ans[i] = [0] + A[i-1][:]
    for j in range(1,W+1):
        ans[i][j] += ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1]

for _ in range(N):
    a,b,c,d = map(int,input().split())
    print(ans[c][d] - ans[a-1][d] - ans[c][b-1] + ans[a-1][b-1])

模範解答では、a = 1 や b = 1 の場合、ans[a-1][d] や ans[c][d-1] や ans[a-1][b-1] が存在しないため、その項を無視するようにコードを書くようになっていますが、ちゃんと ans[0][0] = 0 を作っているので、不要だと思う。

VBA
Sub query_primer__two_dimensions_interval_sum()

    HWN = Split(Cells(1, 1), " ")
    h = Val(HWN(0))
    w = Val(HWN(1))
    N = Val(HWN(2))
    
    Dim A() As Long
    ReDim A(h, w)
    
    For i = 1 To h
        s = Split(Cells(i + 1, 1), " ")
        For j = 1 To w
            A(i, j) = s(j - 1)
        Next
    Next
    
    For i = 1 To h
        For j = 1 To w
            A(i, j) = A(i, j) + A(i - 1, j) + A(i, j - 1) - A(i - 1, j - 1)
        Next
    Next
    
    For i = 1 To N
        yxcd = Split(Cells(i + h + 1, 1), " ")
        y = Val(yxcd(0))
        x = Val(yxcd(1))
        c = Val(yxcd(2))
        d = Val(yxcd(3))
        Debug.Print A(c, d) - A(y - 1, d) - A(c, x - 1) + A(y - 1, x - 1)
    Next
    
End Sub

いつもの如く、境界値データテストで、約 85 秒。Debug.Print をやめると、約 1 秒！ やるな！

最後に

四角い図形を書いて、取りたい区間和部分の色を塗って、どことどこを足せば、引けば、答えが出るだろうと考えます。パズルみたいで面白い。そして、そんな簡単な方法で答えが出てしまうところが、また面白い。

いろいろなパターンで応用可能なので、しっかりと身に付けた方が良いと思っています。LeoSaki（旦那）も似た問題に結構挑戦して、幾何学模様がびっしり書かれたメモ用紙を量産しました！

引き続き、よろしくお願いいたします！

Python学習,Python,paiza

Posted by LeoSaki